Back Propagation 是什麼?
1102 機器學習
這篇文章是看李宏毅老師的影片學習時整理的一些筆記,讓自己複習時方便,文章內容為閱讀清單及上課內容之整理
此篇文章內容均為Back propagation 推導及算法,若是想了解運用的建議閱讀deep learning相關文章喔!
Deep Learning 總整理因為這篇文章會有較多數學算式部分,因此如果不習慣看文章的建議可以直接去看李宏毅老師的影片
點我前往Introduction
Back propagation 誤差反向傳播,簡稱反向傳播,他是一個目前常見用來更新模型梯度的方式,也是深度學習很重要的一個演算法,讓我們可以用有效的方法找到損失函數對於權重的梯度,進而利用Gradient Descent來優化權重
反向傳播最主要的概念就是對所有權重計算損失函數的梯度,再以這個梯度來給予最優更新權重的方法
Update parameters
一開始我們在訓練模型時會有一組初始參數(也就是一堆weight與bias),我們假設叫他為θ
所以θ其實就長這樣:θ={w1, w2, …, b1, b2, …}
接著我們可以計算 θ 對我們 loss function(設為L)的gradient,也就是計算每一個network裡面的參數(w1, w2, … b1, b2, …)對L(θ)的偏微分
計算出這些後,我們稱它為gradient
gradient他其實是一個vector(因為θ裡面有很多參數,每一個都要算偏微分)
有了gradient後我們接著就可以計算新的θ1 = θ - η * gradient (η為learning rate)來更新模型的參數
這樣的process就一直持續下去,可以一直得到新的θ,θ2 = θ1 - η * gradient…
這樣的更新參數的方法跟我們在一般linear regression或其他模型上是沒有差別的
也是把參數帶進loss function裡進行運算後更新參數
只是最大的差別在於在neural network上會有很多的參數需要更新
How to calculate
在一個neural network裡他可能會有上百萬的參數,這代表gradient vector是非常長的(上百萬維度)
因此我們如何有效的將這個vector算出來,這是back propagation主要在做的事
因此他並不是一個「training的方法」,他只是一個有效率的「演算法」,讓你在計算的時候可以更有效率
至於要怎麼算呢? BP裡用到的數學其實不難,就是Chain Rule
Chain Rule
先複習一下什麼是chain rule (不然都還給老師了QQ
假設我們有兩個function : y = g(x), z = h(y)
則若是我們給x一個小變化的話,y和z也會受到影響
所以我們要計算x對z的微分時,我們可以寫成這樣:dz/dx = (dz/dy)*(dy/dx)
若是更進一步,有兩個變數影響一個變數呢,則可以寫成這樣
Substitute
好回到模型上,我們的模型可以簡化成下圖的結構:
x是我們的input,而標準答案是ŷ,透過網路後我們會得到一個y的結果,我們用來評估ŷ和y的差距的函式叫做C
而我們知道我們定義的loss function(L)是所有data的ŷ和y的差距的總和(下圖左邊的等式)
好,整理一下:
x:input
y:模型的output
ŷ:期望的output
C:模型的output和期望的output的差距
L:loss function
則若是我們把這個等式同時都對一變數w做偏微分,就可以得到右邊的式子
有了這個等式後,因為我們知道剛剛在計算gradient就是下圖右邊等式的左邊部分,那這樣我們就可以用計算下圖右邊等式的右邊部分來替代
因此我們在計算gradient上就可以以計算「某一筆data的partial w對partial C的微分」來替代原本total loss 對某一個w的偏微分了~
接下來就只專注在計算「某一筆data的partial w對partial C的微分」
Back propagation
至於要怎麼做呢? 我們先單看一個neuron
我們先拿第一個layer的neuron出來看

從上圖可以得知:
∂C/∂w = (∂z/∂w) * (∂C/∂z) (就是前面提過的chain rule啦!)
我們就把 ∂z/∂w 稱為 forward pass,∂C/∂z 稱為 backward pass
至於爲什麼這樣取名呢? 讓我們繼續看下去~
Forward pass
∂z/∂w 這項不難算,因為我們知道 z = x1w1 + x2w2 + b
則 ∂z/∂w1 = x1, ∂z/∂w2 = x2
這樣我們可以得到一個規律:
∂z/∂w 會等於輸入的x值
好 forward pass結束了 歡呼!!!!!
收!停止歡呼 因為難的要來了…
Backward pass
為什麼 ∂C/∂z 會是魔王呢?

看上面這張圖,若是我們想得到 ∂C/∂z,則我們必須算出這個neuron的output,再進下一層,一直這樣反覆直到最後得到最終網路輸出才可以得到 C (模型理想輸出與實際輸出的差距),所以就得一直往下算很多很多層
設σ為激活函數,則 a = σ(z)

那其實這樣我們又可以用chain rule 把 ∂C/∂z 替換掉:
∂C/∂z = (∂a/∂z) * (∂C/∂a),恩~很好!又拆兩部分了:)
∂a/∂z
我們已知 a = σ(z),因此就可以知道 ∂a/∂z 就是 σ‘(z)(激活函數的微分)∂C/∂a
這項就複雜了
從上面圖片中我們可以得知:
a 會影響 z’ , 接著 z’ 會影響 C
a 會影響 z’’ , 接著 z’’ 會影響 C
上面剛剛講的一會用到,就是用在這裡了!
我們可以接著得出一個式子:
恩很好,是不是開始覺得不如直接算最原本的gradient vector了😂
不行安餒啦 反正是機器算又不是我們手算😁 好繼續!
z’ = aw3 + ….
z’’ = aw4 + …. (點點點就是一坨有的沒的就是了!)
這樣的話有兩項就很好算了:∂z’/∂a = w3,∂z’’/∂a = w4
好~問題來了:因為我們不知道z’ 和 z’’ 對C的影響,那 ∂C/∂z’ 和 ∂C/∂z’’ 到底要怎麼算呢?
不知道怎麼算那我們就假設我們知道答案了
(假設我們已經算出來了,透過等等會講但還不知道怎麼算的算法顆顆)
算出來後,我們的 ∂C/∂z 就會長這樣:
———— 好~分割線分割 ————
接下來你需要想像一下關於我們剛剛「假設」的這件事
我們剛剛是:得知 ∂C/∂z’ 和 ∂C/∂z’’ 因此我們可以推出 ∂C/∂z
所以我們可以把這件事想像成:
有一個neuron叫做σ‘(z)(他不在我們的網路裡),當[ ∂C/∂z’ * w3 + ∂C/∂z’’ * w4 ]這整坨東西經過他後可以得到 ∂C/∂z,如下圖
在上圖中neuron的圖跟下面的等式是同個意思
不過在圖中其實 σ‘(z) 是一個常數,因為在forward pass中 σ‘(z)已經被決定了
所以在這個我們想像的neuron中,他並不是把input做一個non-linear的轉換,因為他是把input乘上一個constant
———— 不要想像,回到現實 ————
那所以那兩項到底要怎麼算呢?
我們現在假設兩個不同的case
- Output layer : 若是在最後一層(z’, z’’經過激活函數後就是整個網路的output)
那所以我們要算 ∂C/∂z’ 和 ∂C/∂z’’ 就很簡單了,第一趴結束!

- Not output layer : 若不在最後一層(後面還有 ∂C/∂za, ∂C/∂zb…)

如圖所示,這樣我們要得知∂C/∂z 就必須要知道 ∂C/∂z’ 和 ∂C/∂z’’,要得知 ∂C/∂z’ 就必須要知道 ∂C/∂za, ∂C/∂zb…就這樣一直持續下去直到我們到output layer
那若是我們有6個neuron,則就會如下圖:
因此當我們在算backward pass時,我們就建一個反向的neuron network,而這個反向的neuron network的activation function我們要先算forward pass後才會得知
每一個反向 neuron 的 input 是 C 對後面一層 layer 的 z 的偏微分 ∂C/∂z ,output 則是 C 對這個neuron的 z 的偏微分 ∂C/∂z,做 Backward pass 就是通過這樣一個反向neural network 的運算,把 C 對每一個 neuron 的 z 的偏微分 ∂C/∂z 都給算出來
挖到這裡,終於結束了好感動
Summary
Forward pass
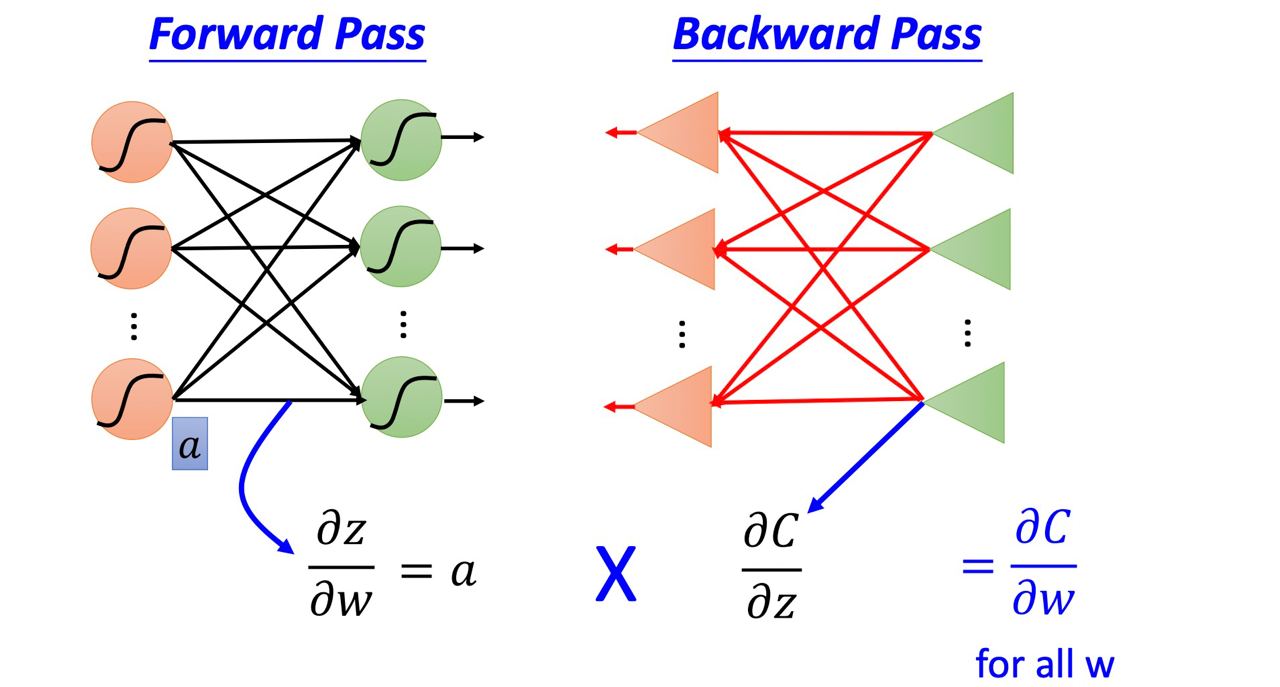
每一個neuron 的activation function 的output,就是他所連結的weight 的 ∂z/∂wBackward pass
建一個與原來方向相反的neural network,它的 neuron 的 output 就是 ∂C/∂z,把通過 forward pass 得到的 ∂z/∂w 和通過 backward pass 得到的 ∂C/∂z 乘起來就可以得到 C 對 w 的偏微分 ∂C/∂w
好感動
在大半夜整理這個筆記的我魂都要沒了
晚安各位~






